flipcode - Realtime Voxel Landscape Engines

Realtime Voxel Landscape Engines - Part 2 - Rendering the Landscape's Structure
by (21 February 2000)

Introduction

The first thing we need to focus on is the processing of the landscape's structure relative to the position of the camera. This involves finding all parts of the landscape that are inside the frustrum, discarding invisible data, and drawing the rest. Before I explain how to do this, let's go through a few basics.

What are Voxels?

A volume element, commonly known as voxel, is similar to a pixel but in 3D. A pixel being a 2D rectangle, a voxel is a 3D box. But unlike pixels, which can take many values, voxels are usually full or empty. Voxels can be used to represent virtually anything, from human skulls in medicine to full 3D worlds. Obviously the more voxels you have, the more precise your model will be. And that's one of the major problems nowadays, there is too little memory to store very complex scenes, so low resolution voxelisations are used. The programmer must therefore use clever algorithms to render the voxelated world in a smooth fashion on the screen.

Using Voxels To Represent Landscapes

The main reason why voxels are commonly used to represent landscapes is simplicity. Indeed, storing a voxelised representation of a landscape is easy, as long as there are no overhangs. In this case, every point in the map has a single altitude. You can then simply store the altitude of each point in a bitmap, which is usually called a height-map. A height-map can have virtually any size, as long as it fits into memory. Sizes of powers of two are of course recommended so that each pixel can be accessed with a bit shift rather than a multiplication.

So we now have an altitude corresponding to each point in our world. To retrieve this value, we can simply read the value from the closest point in the height map, or we can use some kind of filtering. Bilinear filtering which involves computing the weighted average of the 4 neighbouring pixels is usually satisfactory, although we could use the slower bicubic filtering for higher quality engines.

The Raytracing Concept

One method to render a landscape is raytracing. For each pixel, you would compute the equation of the ray that goes through the corresponding point on the projection plane, and then interpolate along that ray to find its intersection with the landscape.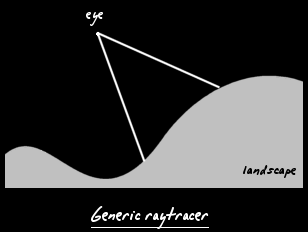

You then only need to plot the pixel with the adequate texture and lighting, which we will discuss later in the tutorial. And that's the generic way to render a voxel landscape. But this method is quite slow on current computers, so we need to find some simplifications to make our engine run quicker. We can also chose to focus more processing time on getting better output quality.

Limited Degree of Freedom

One solution is to limit our engine to four degrees of freedom. This means that the camera would not be able to look up or down, or tilt side by side. The four degrees of freedom being the three translations, and the rotation around the Y axis. This limitation is fairly annoying, especially if you want to use the engine in a game, but it makes the rendering algorithm that much more efficient. So if you can put up with limited movement, you'll be able to get much more quality.

Raycasting

So by limiting the movement, we make sure that the upper part of the view frustrum is always directly above the lower part of the frustrum. This way, all the rays in the same column project onto the same line in the height map.

The obvious thing to do is to make sure we interpolate only once for each ray in the same column. As you'll quickly realise, this is extremely simple.

Wave Surfing

Let's consider a single column of pixels. As we saw previously, we can associate to it a ray through the heightmap. We start the interpolation at the origin, where the camera is. Then at regular intervals along the ray, we retrieve the altitude from the heightmap, and project that onto the screen with the standard projection equation:

Ys = ( Yv - Ye ) * Yk / Z + Yc

Ys: coordinate projected onto the screen
Yv: altitude of the voxel column
Ye: coordinate of the eye
Z: distance from the eye to the considered point
Yk: constant to scale the projection, possibly negative
Yc: constant to centre the projection, usually half the screen resolution

Having computed the coordinate of the projection point, we compare that with the highest point drawn so far. If it's higher, then the column of voxels is visible so we draw it.

This diagram should make things clear. When we start interpolating, the voxels aren't visible on the screen. Then we continue scanning along the ray until the voxels project onto the screen. They will remain visible until the landscape dips, at which point we interpolate without drawing. We just surf along to the next mountain, and draw that. So the visible mountains will get higher and higher on the screen, but most likely they will average out at the middle of the screen, where the horizon is. If we ever get to the top of the screen, we can stop interpolating since however high the following mountains are, they will never be visible.

Two Different Approaches

There are basically two approaches to tracing all your rays. The first is to trace one ray right to the end and then move onto the next one, the other approach is similar to texture mapping since you interpolate along a depth line, thereby scanning all the rays at the same time.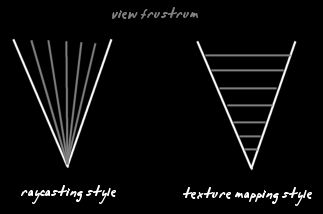

After a lot of thinking about this topic, I realised that both methods have advantages in different cases:

Raycasting style
+ no need to remember variables for all other rays
- constant depth optimisations must be precomputed

Texture mapping style
+ constant depth optimisations can be computed in realtime, and only once for each depth line
- need to store deltas and occlusion information for each ray

The choice all depends what features you need to implement in your main rendering loop. One method could be much more efficient than the other.

The Algorithm

This algorithm is based on the raycasting style method. Converting to the texture mapping style shouldn't be to hard at all.


     for i from 0 to RESX do loop
         get the equation of the ray
         for j from MIN_DIST to MAX_DIST do loop
             find the point in the map
             get its altitude, and project it onto the screen
             if it's above the highest point drawn so far
                if the previous point was invisible clip the span
                draw a vertical span from the previous point to the current point
                set the highest point to be the current point
             end if
             exit the loop if the highest point is above the screen
         end loop
     end loop

A more detailed explanation of how to actually render the spans is provided in the next section.

Article Series:

Realtime Voxel Landscape Engines - Part 1 - Introduction
Realtime Voxel Landscape Engines - Part 2 - Rendering the Landscape's Structure
Realtime Voxel Landscape Engines - Part 3 - Texture and Lighting
Realtime Voxel Landscape Engines - Part 4 - Level of Detail and Optimisation
Realtime Voxel Landscape Engines - Part 5 - Quality Improvement
Realtime Voxel Landscape Engines - Part 6 - Hardware Acceleration
Realtime Voxel Landscape Engines - Part 7 - The Engine
Realtime Voxel Landscape Engines - Part 8 - Final Words