|
Plücker Coordinates for the Rest of Us - Part 1 by Lionel Brits (15 November 2001) |
Return to The Archives |
Introduction
 |
| When I first happened upon articles dealing with Plücker Coordinates I found it hard to interpret the mathematical expressions geometrically and many of the ideas were intimidating. Since I couldn't find any lighter material on the subject I put off familiarizing myself with the concepts for more than a year. I then revisited the articles but still found them full of big words and unfamiliar notation, so I tried to imitate, by my own means, what Plücker coordinates promised: a way of mathematically describing the relative orientations of lines. After spending a few hours trying to make my scribblings on paper look 3D I ended up with expressions that looked suspiciously like those I had seen in the other articles. After a few more hours of scribbling my arrogance got the best of me and I decided to contribute my own article to the white noise that is the world wide web. Lo and behold, you are reading that very article. Good luck. |
A Word on Convention
 |
For the sake of consistency we will be using the the right-hand coordinate
system throughout this discussion.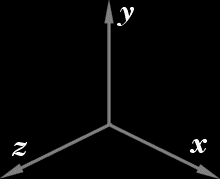 Also, I chose notations to be reasonably consistent with other sources whenever possible. |
Defining a Line in 3-Space
 |
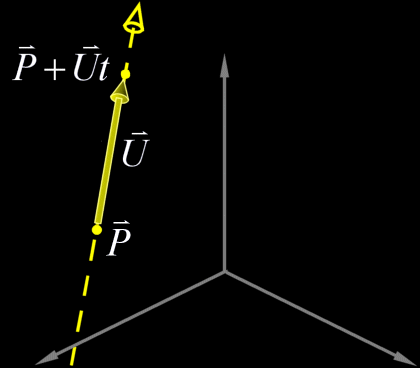
All we need to define a line in 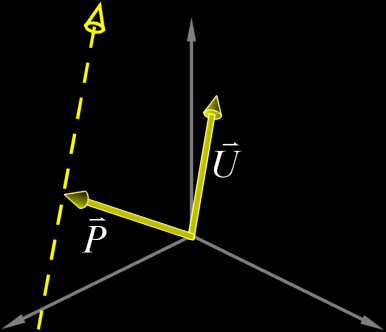 Any point |
Relative Orientation
 |
What we also need is a way to determine the relative orientation
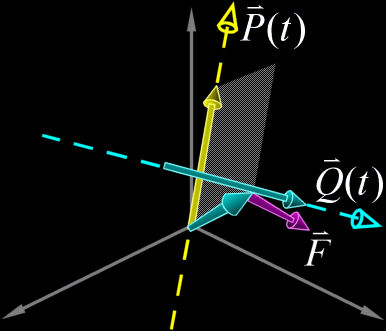
of two lines. Electromagnetic theory gives us a convenient way to express the
orientation of a line in terms of the Biot-Savart law. This law gives us the
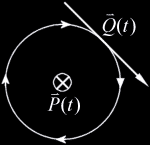
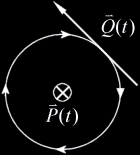
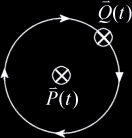
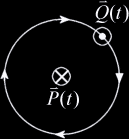
magnitude and direction of the magnetic field 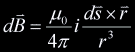 This formula is however too intimidating for our purposes so we will strip from it everything but the bare essentials. The familiar Right-Hand rule gives us a non-mathematical way of finding the direction of the field  In the same way we can define a direction around a line. We will follow the convention that when looking along a line in the direction of the line, other lines are either oriented clockwise (CW), counterclockwise (CCW), or intersect or are parallel to the line being viewed. In the following example lines 2 and 3 are moving clockwise around line 1. 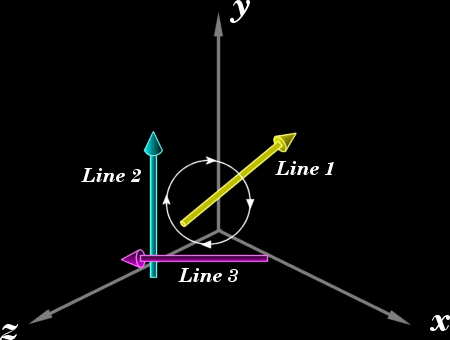 This is analogous to the direction of the magnetic field 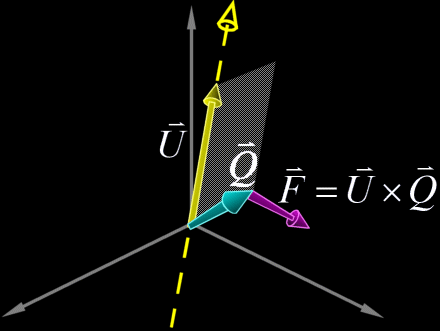 Now we have a powerful way of finding information about the orientation of lines relative to
We can express these cases in terms of the dot product of
Note: There is some ambiguity in the case of We ought now to generalize these cases given that The vector value of Which is equivalent to The orientation we are interested in we can call Which is equivalent to This expression on its own is sufficient for allowing us to express the relative orientations of lines in Given two lines If If If |
Clocks and Hands and Lines Oh My!
 |
| It doesn't end here, however. If you think you have what it takes, take a stroll through the next installment. |
|
Article Series:
|