 |

Submitted by , posted on 07 December 2001
|
 |
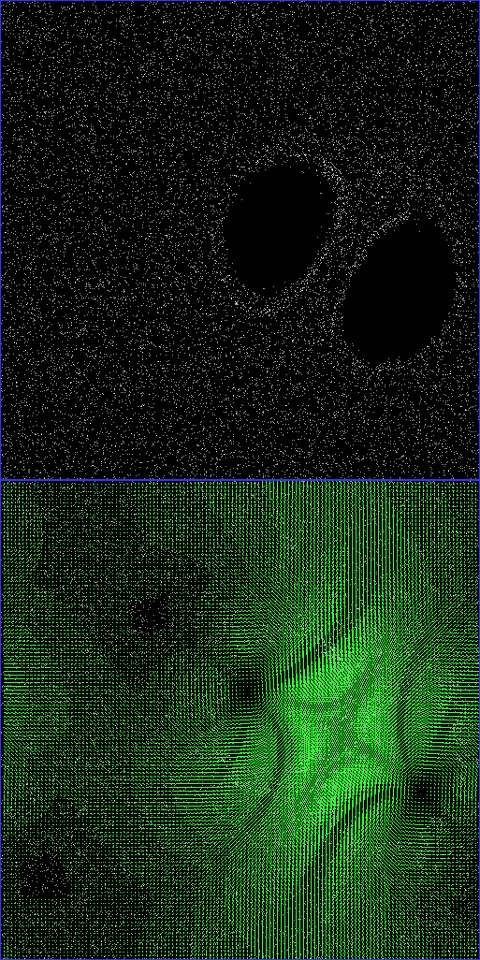
Image Description, by

These two images show my fluid simulator in action. There are over 16000
particles suspended in the liquid. The liquid can be modified by applying
external forces with the mouse. The liquid is defined on a 128x128 grid.
Unfortunately I had to remove the FPS and other information from the borders
of the screenshots in order to get the IOTD to fit. But it runs at just
under 30fps on an 800Mhz P3.
The top screenshot shows two vortices forming after a single force was
applied across the liquid.
The lower screenshot shows the fluid velocities at each cell.
The simulator solves the Navier-Stokes equations. These equations were
defined more than 150 years ago by Claude Navier and George Stokes. These
equations express the evolution of the liquid's state over time. That is to
say, the equations describe how much the liquid has changed over a discrete
period of time, as opposed to defining it's state at an arbitrary time. The
problem is that the equations are highly non-linear which makes them
incredibly hard to solve accurately and efficiently.
The solver that I am using was developed by Jos Stam, a researcher at
Alias|Wavefront. He originally published a paper entitled "Stable Fluids" at
SIGGRAPH 1999. The maths in the paper is very hairy, and the paper assumes a
good grounding in fluid dynamics. I have neither a good grounding in maths,
or an understanding of fluid dynamics (not beyond drinking anyway)! You can
find the SIGGRAPH paper at Stam's website -
http://www.dgp.utoronto.ca/people/stam/reality/Research/pub.html
If, however, you make the boundaries of the fluid periodic and remove
support for obstacles in the fluid you can simplify several calculations by
using the Fourier domain (and it's associated transform the FFT), which
allows you to achieve real-time computation. This is the basis of the solver
that Stam describes in an article to be published in the Journal of Graphics
Tool. That article is available on his website here -
http://www.dgp.utoronto.ca/people/stam/reality/Research/pub.html.
In fact he
even provides source code for the solver in the article! His source code is
what I used to create my solver.
Jos Stam should take all the credit, I just strapped a user interface and
D3D shell onto the front of it!
I recommend anyway whose is interested in learning about different aspects
of computer graphics to at least read the JGT article. In addition I would
recommend that people investigate the Fast Fourier Transform. The FFT is a
very powerful tool with many uses in computer graphics - generating tiling
textures, landscape synthesis, efficient evaluation of the summation of many
sin/cos functions, to name but a few.
Finally - the simulator makes for a great toy, and I have a screensaver
version of this in the works. :)
Chris Killpack
|
|

