 |

Submitted by , posted on 13 May 2002
|
 |
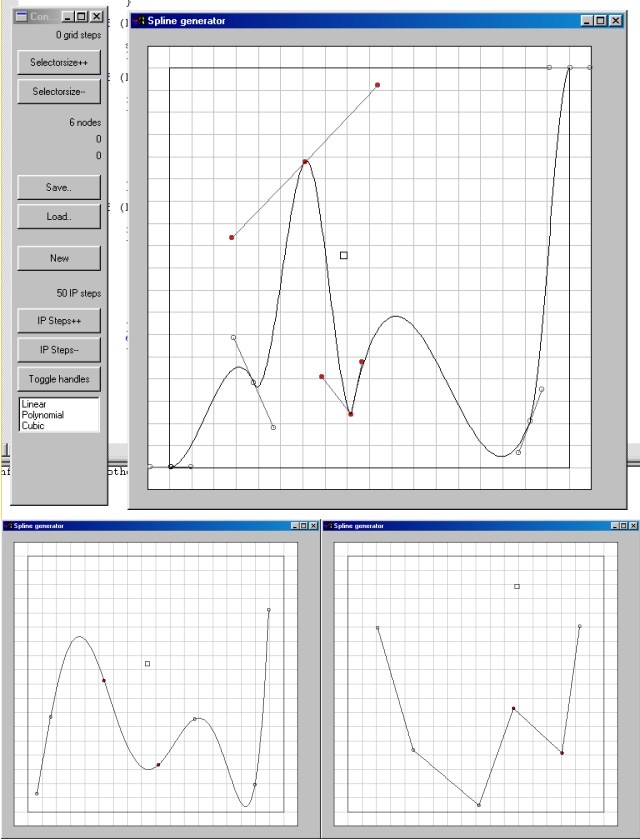
Image Description, by

I like making gametools. (And demo tools), and they are apparently a
little rare here on IOTD, so I'll post my most recent one.
It's a spline editor with support for 3 types of splines.
Regular linear splines (extremely boring :)
Polynomial splines
Cubic splines.
In the top image you can see the control panel and the editor window
with a cubic spline. The bottomleft is a polynomial spline, and the
bottomright is a linear spline. In the cubic spline image, you can see
the handles attached to each node, and you can see some broken handles.
(i.e. 2 handles connected to the same node, but which can be moved
independently).
Cubic splines are the most interesting, as they provide the best control
of the exact shape of the generated curve. Those of you who uses 3D
animation systems probably knows their use in the form of camerapathing
and object movevement as well as a lot of other nifty applications.
Polynomial splines uses an N-degree polynomial to interpolate the
points. That is, if there are 5 points, the interpolating spline will be
a 5-degree polynomial. This has some (dis)advantages, depending on the
use, namely that the constructed spline depend on all data points, and
that we get some nasty looking splines with high degree polynomials.
However, the first derivative at each point isn't needed as it is in
cubic splines. This implementation uses the Newton divided differences form
The cubic spline solves the problem that high degree polynomial splines
has. By explecitly specifying the first derivative at each point, we get
an interpolating spline which in any given subinterval is dependent
solely on it's two closest points. As such, cubic splines provide a
continuous interpolant which is indifferent wrt. the rest of the data
points. I.e. You can modify/specify all other datapoints without
altering the rest of the curve. I used the Hermite form in the
implementation.
In the editor you can of course move, add and remove nodes, and you can
move and break handles. The calculated spline itself is drawn by
dividing each subspline into a number of interpolation steps (on the
IOTD it is 50) and connecting them with straight lines.
/Simon Reinholt
You can download the editor here: iotd-05-13-2002_splinegenerator.zip
NOTE: If you download the editor, you'll notice a lot of flickering.
This is a Quick-N-Dirty(TM) program coded solely out of interest for
spline interpolation. Hopefully there aren't too many bugs in it. :)
|
|

