|
3D Geometry Primer: Chapter 1 - Issue 05 - 3D Space: Righthanded Rules, And More... by (11 September 2000) |
Return to The Archives |
3D Space: Righthanded Rules, And More...
 |
| Today we're going to examine what the benefits are of a righthanded base, what the rule of the corkscrew is, and how you should draw 3D bases on paper. |
(I) Two Ways To Arrange Those 3D Bases
 |
|
I don't know if you have noticed it yet, but there are two ways to set up the
bases we saw last week: lefthanded and ... righthanded, of course. Let me
explain... Everybody, take 2 sets of 3 pencils: 2 red, 2 green and 2 blue ones. Each pencil will represent a base vector (red = I, green = J and blue = K). The top of the pencils (the side that writes) will be their heads and the back of them are the tails and are gathered in the origin O. Take a red (I) and a green (J) pencil and hold them perpendicular in one hand, and do this also for the other red and green pencil in your other hand. We've got 2 times 2D space now: once in your left hand, and once in your right. And they are both the same thing! Whatever you do, as long as I and J are perpendicular, you always will be able to lay both "spaces" upon each other so that they match: origin[1] matches origin[2], I[1] matches I[2] and J[1] matches J[2]. (the index [1] or [2] refer to the pencil in your left or right hand respective.) Now, we'll have to extend our 2D space with a 3rd base vector K (blue pencil) and create a 3D space. How can you do that? Two ways: or you aim the K vector downwards, or upwards (at least, if you're holding your 2D spaces horizontal). If you aim K[1] downwards, and K[2] upwards, then you'll see that you won't be able to match both spaces anymore. We've create 2 totally different worlds! 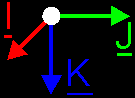 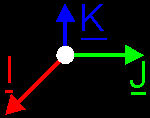 What about the left- and righthanded? Well, if you represent I by your thumbs, J by your index finger and K by your middle finger; then you will see that you can represent both systems with you left- and righthand: you'll find out that you've created two 3D spaces like above (you will have to turn the stuff a little...). And you won't be able to let match both spaces neither. 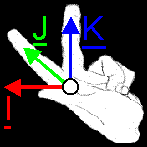 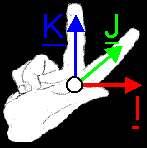 We have a problem now: we've got 2 kinds of 3D spaces: which one to chose? You're free to do what you want, but normally in math, the righthanded one is used. It's not a discrimination against lefthanded people, it's just a habit, an agreement. So, remember, if you have to imagine your I,J,K 3D-world: take you righthand and count "I J K" on your fingers. In a few weeks, we'll see that this I,J,K world can be extended to our normal cartesian XYZ world, and the same thing will apply on that: you will count "X Y Z" on your righthand. |
(II) That Cross Product Again
 |
|
You remember this from last week? I×J = K J×K = I K×I = J Now, look again at the cross product (issue I.02, (vi)), take your righthanded base {I,J,K}, and try to construct each cross product I×J, J×K, K×I. Pay attention to that hand! Notice that the magnitudes are correct too: all magnitudes are 1, and sin(90°)=1 too. Put this in your head. Now! |
(III) The Rule Of The Righthanded Corkscrew
 |
|
very, Very, VERY, *VERY* IMPORTANT! Now something about contours of polygons or 2D shapes in general. Say, we have a polygon and we need to store it's vertices in an array (we don't know how to do this yet, but say that we could... :). We'd like to do it in a way such that we can run through the vertices, and in that way follow the contour of the polygon. The question is: in what way do we need to store the vertices, to be compatible with other things in our environment? First, another thing: I think that we all know that we can run in a circle in 2 ways: clockwise and counter-clockwise. But how do we decide which way is the one and which is the other? If you take a clock (of which the pointers go clockwise...), and you look from the back, you'll notice that the pointers run counter-clockwise! So it all depends from which side you're looking. To solve the problem, it's very simply: we say that, in 3D, each polygon has a front and a back (like a clock does). Now, there's still the problem of storing the vertices: shall we do it clockwise or counter-clockwise? Take a convex 3D polygon (ABCD...Z), and use a point in the middle of it as the "centre". Call that point M. It doesn't has the be the real centre of the polygon, as long as it is in the polygon. The front of the polygon is the upper side (the side you see). 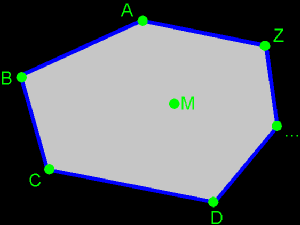 From that point M, you pull vectors to each vertex: MA, MB, ..., MZ 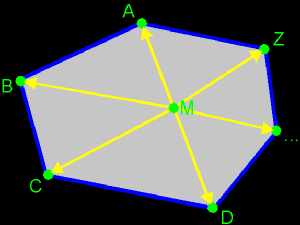 We pick 1 vertex to start with, let it be A. This will be the first vertex of our "storage sequence": P[0]. Now, we want to store the next vertex P[1]. One thing is sure, it has to be a neighbour of A. But shall we pick B or Z? To decide that, we construct both cross products MA×MB and MA×MZ. We find out that the first one MA×MB pops to the front, and the second one sticks to the back. We choose to take the first one, because of that "to the front" thingy. 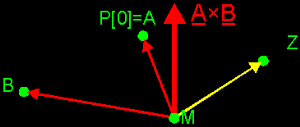 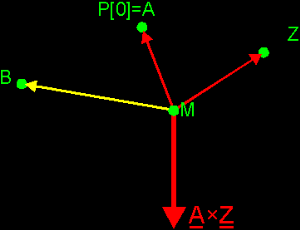 We have P[1]=B now. What will be P[2]? Of course, we can't take A because it's stored already, so we need to pick C. And so on, until you reach Z. But even if you would decide this with the cross products, then you would find out that you need to choose C. In fact, for each 2 succesive points P[i] and P[i+1] you take, you will find out that MP[i]×MP[i+1] sticks to the front. Try this out!  And all these cross products are perpendicular to the surface of the polygon. These is logical, because MP[i] and MP[i+1] lay in that surface, so MP[i]×MP[i+1] must be perpendicular to the polygon. Between all vectors that are perpendicular to a polygon, there's 1 special: the normal vector: ° it is perpendicular to the surface ° it has magnitude 1 (it's normalized) ° it sticks out to the front ° it has the same direction and sense like each MP[i]×MP[i+1] ° it's called N This normal vector is something you need to remember. You will use it often. Just imagine it as a unit vector that starts somewhere in the polygon (it doesn't matter where exactly) and stands perpendicular to that surface. You can remember all this in short with next image. You simply imagine the normal vector of the polygon and you lay your right thumb along it. Now if you close your hand, you will find the sequence in which you need to store the vertices. Or otherwise, if you close your hand in "correct" way, you find the normal vector with your thumb. Also, this "hand" trick can be used on concave polygons. The trick with the cross products can't. Can you see why? 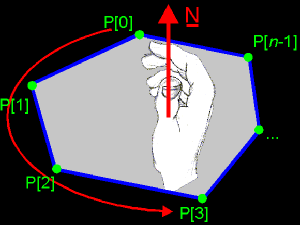 What has this to do with a corkscrew? Well, some people use the following trick, if you want your corkscrew to go in the N sense, you need to turn it in the given way. Or something like that... Anyway, everybody knows the hand-trick as the rule of the corkscrew. Of course, if you're working in a lefthanded system, you need to use your left hand instead of the right one... |
(IV) How To Draw A 3D Base On 2D Paper Correctly?
 |
Basically you can lay your base vectors in any way you want. The only thing you
should keep in mind, is that you draw the base vectors from I to
K in counter-clockwise order (and again...). That will be the
most natural way. Of course, if you want to draw a lefthanded space, you do it
clockwise. 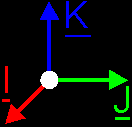 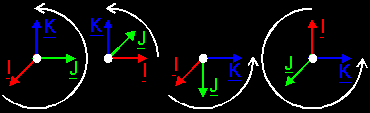 There's also another way if you're only interested in 2 of the 3 base vectors. For example, when you're currently working with a situation in which the z-value of all points is 0 (zero), then you're not interested in the K vector. The z-value is 0 anyway. So, you only need the I and J vectors. The way to do that, is to draw the K vector perpendicular to your paper. *Yoink?* How do you that? Well, you can't draw a vector really perpendicular to your paper, so you project it. Just like you would do in other cases. But the projection of a perpendicular vector is just 1 point! How do you see if the vector sticks in the paper, or comes out of it? Simple. If you point a real arrow (of an archer) into your paper, what do you see? Correct, the tail of the arrow. So you draw the tail (with those feathers). That is a little cross in a circle. And what if you point the arrow in the other sense? You see the head of the arrow, the sharp point of it. So you draw that, and this is a little ball (the sharp point...) in a circle. Voila, if you use your imagination, everything comes clear... 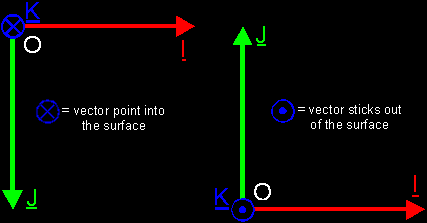 |
(V) Why Is The Origin Of The Screen In The Upper-Left Corner?
 |
Have you ever wondered why the heck the origin of the screen is in the
upper-left corner, while normally it should be in the lower-left corner like in
math? I did. I don't have a real answer to it, but I did notice one nice
thing. If you take a righthanded space and lay it's origin in that one of the
screen, lay the I and J vectors aside those ones of the screen,
then you will find out the the K vector will point into the screen. Just
like we want in 3D-engines: the camera in the origin and lays aside K.
Isn't that very handy? (Or maybe we want to point the camera that way,
because the screen is made that weird. I don't know...) So, if you should have a weird screen with its origin in the lower-left corner, you could decide to use a lefthanded 3D space, because then the K vector will point into the screen again. But beware! If you do that, you need to turn around the whole thing: every righthanded becomes lefthanded and every counter-clockwise because clockwise, and vice versa (or something ...). |